23-02-2021
Vectors
I think of the dot product as directional multiplication. Multiplication goes beyond repeated counting: it's applying the essence of one item to another.
Dot product: Apply the directional growth of one vector to another. The result is how much stronger we've made the original vector (positive, negative, or zero).
Mario-Kart Speed Boost Analogy
In Mario Kart, there are "boost pads" on the ground that increase your speed. (Never played? I'm sorry.)

Imagine the red vector is your speed (x and y direction), and the blue vector is the orientation of the boost pad (x and y direction). Larger numbers are more power.
How much boost will you get? For the analogy, imagine the pad multiplies your speed:
If you come in going 0, you'll get nothing (if you are just dropped onto the pad, there's no boost)
If you cross the pad perpendicularly, you'll get 0 (it will give you 0x boost in the perpendicular direction).
But, if we have some overlap, our x-speed will get an x-boost, and our y-speed gets a y-boost:
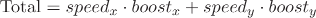
Neat, eh? Another way to see it: your incoming speed is |a|, and the max boost is |b|. The percentage of boost you actually get (based on how you're lined up) is 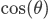 , for a total of
, for a total of  .
.
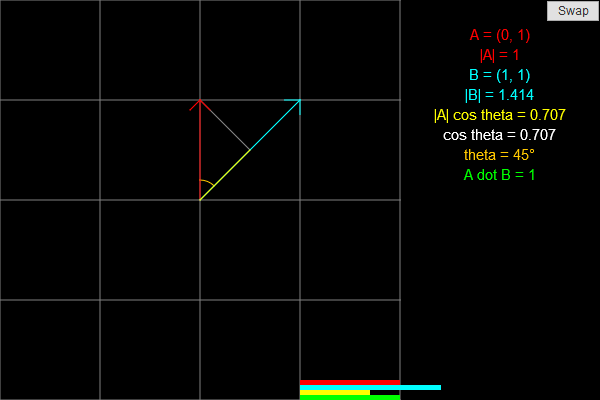
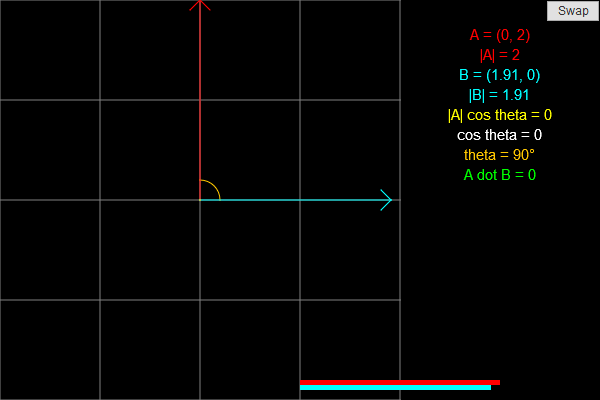
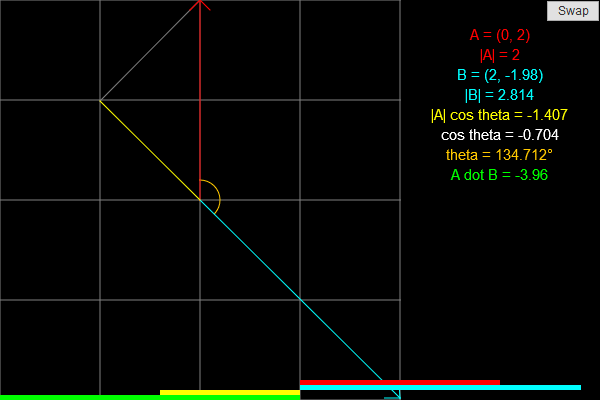
This applet demonstrates the dot product, which is an important concept in linear algebra and physics. The goal of this applet is to help you visualize what the dot product geometrically.
Two vectors are shown, one in red (A) and one in blue (B). On the right, the coordinates of both vectors and their lengths are shown. The projection of A onto B is shown in yellow, and the angle between the two is shown in orange.
At the bottom of the screen are four bars which show the magnitude of four quantities: the length of A (red), the length of B (blue), the length of the projection of A onto B (yellow), and the dot product of A and B (green). Some of these quantities may be negative.
To modify a vector, click on its arrowhead and drag it around. To swap A and B, click the swap button. Swapping the two does not change the dot product.

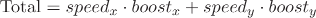
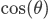 , for a total of
, for a total of  .
.


